初中数学 第十九课时：二次函数的应用

概要： B.0.4 C.0.3 D.0.6【考点归纳】1. 二次函数的解析式：(1)一般式：( );(2)顶点式：( ) ;(3)交点式：( ).2. 顶点式的几种特殊形式.线( )对称，顶点坐标为( ， ).⑴ 当a>0时，抛物线开口向( ) ，有最( )(填"高"或"低")点, 当X= ( )时， 有最( )("大"或"小")值是( ) ;⑵ 当a<0时，抛物线开口向( )，有最( )(填"高"或"低")点, 当X=( )时， 有最( )("大"或"小")值是( ).【典型例题】例1 橘子洲头要建造一个圆形的喷水池，并在水池中央垂直安装一个柱子OP，柱子顶端P处装上喷头，由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示).若已知OP=3米，喷出的水流的最高点A距水平面的高度是4米，离柱子OP的距离为1米.(1)求这条抛物线的解析式;(2)若不计其它因素，水池的半径至少要多少米，才能使喷出的水流不至于落在池外?6. 下列函数关系中，是二次函数的是( )A.在弹性限度内，弹簧的长度y与所挂物体质量x之间的关系B.当距离一定时，火车行驶的时间t与

编者按：www.guaimaomi.com小编为大家收集了“初中数学 第十九课时：二次函数的应用”，供大家参考，希望对大家有所帮助!

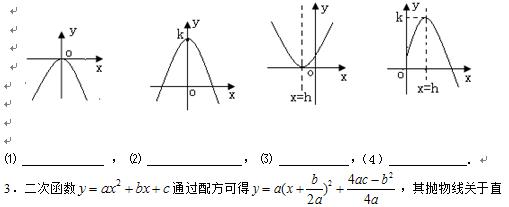
2. 有一个抛物线形桥拱，其最大高度为16米，跨度为40米，现在它的示意图放在平面直角坐标系中(如右图)，则此抛物线的解析式为(     ).

3. 某公司的生产利润原来是a元，经过连续两年的增长达到了y万元，如果每年增长的百分数都是x，那么y与x的函数关系是(     )

4. 把一段长1.6米的铁丝围长方形ABCD，设宽为x，面积为y.则当y最大时，x所取的值是(     )

A.0.5      　B.0.4     　　　　 C.0.3     　　　  D.0.6

【考点归纳】

1. 二次函数的解析式：(1)一般式：(     );(2)顶点式：(     ) ;(3)交点式：(     ).

2. 顶点式的几种特殊形式.

线(     )对称，顶点坐标为(        ，         ).

⑴ 当a>0时，抛物线开口向(     ) ，有最(     )(填"高"或"低")点, 当X= (     )时， 有最(     )("大"或"小")值是(     ) ;

⑵ 当a<0时，抛物线开口向(     )，有最(     )(填"高"或"低")点, 当X=(     )时， 有最(     )("大"或"小")值是(     ).

【典型例题】

例1 橘子洲头要建造一个圆形的喷水池，并在水池中央垂直安装一个柱子OP，柱子顶端P处装上喷头，由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示).若已知OP=3米，喷出的水流的最高点A距水平面的高度是4米，离柱子OP的距离为1米.

(1)求这条抛物线的解析式;

(2)若不计其它因素，水池的半径至少要多少米，才能使喷出的水流不至于落在池外?

6. 下列函数关系中，是二次函数的是(　　 )

A.在弹性限度内，弹簧的长度y与所挂物体质量x之间的关系

B.当距离一定时，火车行驶的时间t与速度v之间的关系

C.等边三角形的周长C与边长a之间的关系

D.圆心角为120°的扇形面积S与半径R之间的关系

以上就是www.guaimaomi.com为大家提供的“初中数学 第十八课时：二次函数及其图像”希望能对考生产生帮助，更多资料请咨询www.guaimaomi.com中考频道。