初中数学 第二十一课时：函数的综合应用（2）

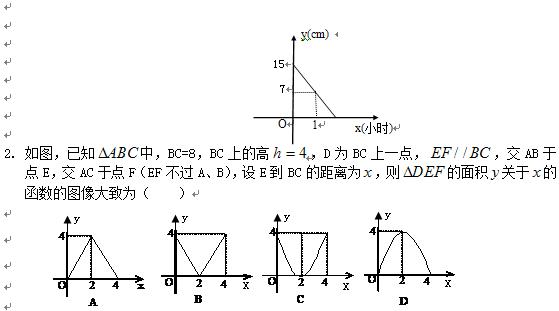
概要：量相应减少10个.⑴ 假设销售单价提高x元，那么销售每个篮球所获得的利润是___________元;这种篮球每月的销售量是___________个.(用含x的代数式表示)⑵ 当篮球的售价应定为___________元时，每月销售这种篮球的最大利润，此时最大利润是___________元.【考点归纳】【典型例题】例1 近年来，"宝胜"集团根据市场变化情况，采用灵活多样的营销策略，产值、利税逐年大幅度增长.第六销售公司2004年销售某型号电缆线达数万米，这得益于他们较好地把握了电缆售价与销售数量之间的关系.经市场调研，他们发现：这种电缆线一天的销量y(米)与售价x(元/米)之间存在着如图所示的一次函数关系，且40≤x≤70.(1) 根据图象，求y与x之间的函数解析式;(2) 设该销售公司一天销售这种型号电缆线的收入为w元.① 试用含x的代数式表示w;② 试问当售价定为每米多少元时，该销售公司一天销售该型号电缆的收入最高?最高是多少元?例2 随着绿城南宁近几年城市建设的快速发展，对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润 与投资量 成正比例关系，如图(1)所示;种植花卉的利润 与投资量 成二次函数关系，如图(2)所示(注：利润与投资量的单位：万元)⑴ 分别求出利润 与 关于投资量 的函数关系式;⑵ 如果这位专业户以8万元资金投入种植花卉和树木，他至少获得多少利润?他能获取的最大利润是多少?以上就是www.guaima

编者按：www.guaimaomi.com小编为大家收集了“初中数学 第二十一课时：函数的综合应用(2)”，供大家参考，希望对大家有所帮助!

【课前复习】

1.如图是某种蜡烛在燃烧过程中高度与时间之间关系的图像，由图像解答下列问题： ⑴ 此蜡烛燃烧1小时后，高度为___________cm;经过___________小时燃烧完毕;⑵ 这个蜡烛在燃烧过程中高度与时间之间关系的解析式是___________.

3. 某商场购进一种单价为40元的篮球，如果以单价50元售出，那么每月可售出500 个.根据销售经验，售价每提高1元，销售量相应减少10个.

⑴ 假设销售单价提高x元，那么销售每个篮球所获得的利润是___________元;这种篮球每月的销售量是___________个.(用含x的代数式表示)

⑵ 当篮球的售价应定为___________元时，每月销售这种篮球的最大利润，此时最大利润是___________元.

【考点归纳】

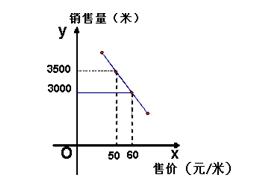
【典型例题】

例1 近年来，"宝胜"集团根据市场变化情况，采用灵活多样的营销策略，产值、利税逐年大幅度增长.第六销售公司2004年销售某型号电缆线达数万米，这得益于他们较好地把握了电缆售价与销售数量之间的关系.经市场调研，他们发现：这种电缆线一天的销量y(米)与售价x(元/米)之间存在着如图所示的一次函数关系，且40≤x≤70.

(1) 根据图象，求y与x之间的函数解析式;

(2) 设该销售公司一天销售这种型号电缆线的收入为w元.

① 试用含x的代数式表示w;

② 试问当售价定为每米多少元时，该销售公司一天销售该型号电缆的收入最高?最高是多少元?

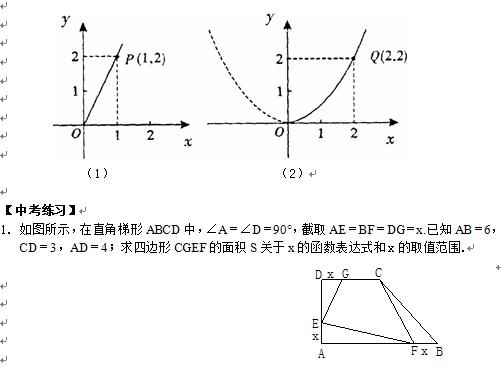
例2  随着绿城南宁近几年城市建设的快速发展，对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润 与投资量 成正比例关系，如图(1)所示;种植花卉的利润 与投资量 成二次函数关系，如图(2)所示(注：利润与投资量的单位：万元)

⑴ 分别求出利润 与 关于投资量 的函数关系式;

⑵ 如果这位专业户以8万元资金投入种植花卉和树木，他至少获得多少利润?他能获取的最大利润是多少?

以上就是www.guaimaomi.com为大家提供的“初中数学 第二十一课时：函数的综合应用(2)”希望能对考生产生帮助，更多资料请咨询www.guaimaomi.com中考频道。