“相似三角形的性质”教学片断

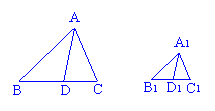
概要：证这两个三角形相似，具备了哪些条件，还差哪些条件?请大家写出证明过程(此时大多数学生已能找到证题思路)证明：∵ΔABC∽ΔA1B1C1，∴∠B=∠B1又∵AD是BC边上的高，A1D1是B1C1边上的高∴∠ADB=∠A1D1B1=90°∴ΔABD∽ΔA1B1D1(AA)∴==k师：请大家用语言来总结这个结论?生：相似三角形的对应高的比等于相似比。邓亚平：老师，我认为还可以总结得更一般点?师：说说你的想法?邓亚平：相似三角形的一切对应线段的比都等于相似比。师：你们大家的看法呢?生众：可以这样总结，我们也是这样认为的。师：首先对这种思考方式表示赞赏，非常不错的。但要说明的是，根据一些特殊的结论来进行推广，属于我们合情推理的一部分，但这种推理有些是正确的，而有些会产生错误。能不能再举一点例子说明你们这个结论的正确性?生：还有对应角平分线与中线可以用来证明这个结论(情绪高涨)。师：好的，来看一看，如何证明?如图所示，如果ΔABC∽ΔA1B1C1，AD是∠BAC 的角平分线，A1D1是∠B1A1C1的角平分线，且=k，试证：==k。生：简单，证得∠BAD=∠B1A1D1即可。师：大家在学习新东西的时候切勿眼高手低，一定要塌实的完成例题，否则很容易导致失误。另外数学的书写格式很重要，特别对于考试来说，步骤是按步得

如图所示，如果ΔABC∽ΔA1B1C1，AD是BC边上的高，A1D1是B1C1边上的高，且

=k，请大家猜想：

与相似比有何关系?

生：

=

=k

师：猜想要经过证明才能作为结论使用，请大家想一想，如何证明?

(留几分钟给学生思考)

分析：在这里要通过三角形相似去证比例式，先要看所证的比例式在哪两个三角形中，在这里是在ΔABD与ΔA1B1D1中，只需要证这两个三角形相似即可。再想想：要证这两个三角形相似，具备了哪些条件，还差哪些条件?

请大家写出证明过程(此时大多数学生已能找到证题思路)

证明：∵ΔABC∽ΔA1B1C1，

∴∠B=∠B1

又∵AD是BC边上的高，A1D1是B1C1边上的高

∴∠ADB=∠A1D1B1=90°

∴ΔABD∽ΔA1B1D1(AA)

∴

=

=k

师：请大家用语言来总结这个结论?

生：相似三角形的对应高的比等于相似比。

邓亚平：老师，我认为还可以总结得更一般点?

师：说说你的想法?

邓亚平：相似三角形的一切对应线段的比都等于相似比。

师：你们大家的看法呢?

生众：可以这样总结，我们也是这样认为的。

师：首先对这种思考方式表示赞赏，非常不错的。但要说明的是，根据一些特殊的结论来进行推广，属于我们合情推理的一部分，但这种推理有些是正确的，而有些会产生错误。能不能再举一点例子说明你们这个结论的正确性?

生：还有对应角平分线与中线可以用来证明这个结论(情绪高涨)。

师：好的，来看一看，如何证明?

如图所示，如果ΔABC∽ΔA1B1C1，AD是∠BAC 的角平分线，A1D1是∠B1A1C1的角平分线，且

=k，试证：

=

=k。

生：简单，证得∠BAD=∠B1A1D1即可。

师：大家在学习新东西的时候切勿眼高手低，一定要塌实的完成例题，否则很容易导致失误。另外数学的书写格式很重要，特别对于考试来说，步骤是按步得分，如果有跳步现象就是要被扣分，如果有重复书写，就是浪费了时间。所以还是请大家认真写出证明过程来。

生：∵ΔABC∽ΔA1B1C1，

∴∠BAC=∠B1A1C1

又∵AD是∠BAC 的角平分线，A1D1是∠B1A1C1的角平分线

∴∠BAD=

∠BAC，∠B1A1D1=

上一页  [1] [2] [3]  下一页