解较复杂的应用题应从哪里入手[04-24 22:23:04] 来源:http://www.guaimaomi.com 解题研究 阅读:9479次
概要:即1500·(72+6+72)=10(分钟)。从出发到相遇,狗每分钟跑300米,甲、乙两人相遇时,狗共跑了300×10=3000(米),即3千米。2从整体构造入手。例2 甲、乙两列火车分别从A、B两城同时相对开出。经过5小时相遇。列车分别到达B、A城后,各休息2小时,再往回开。已知两列火车往返中速度不变,问从原地出发到第二次相遇,共经过多少小时?分析与解:按照常规思路,设未知数列方程。将会碰到较大麻烦。现从整体上考虑,两列火车从开始到第二次相遇共走了A、B 间的三个单程,而合走一个单程要5小时,所以共需要5×3+2=17(小时)。3从份数入手。例3甲管注水速度是乙管的一半,同时开放甲、乙两个水管向池中注水,16小时可以注满。现在先开甲管向池中注水若干小时,剩下的由乙管注10小时将池注满。问:甲管注水的时间是多少小时?分析与解:设甲管1小时的注水量为1份,则甲、乙两管的注水量为(1+2)×16=48(份)。因为乙管10小时注水2×10=20(份),所以甲管先注水48-20=28(份),即甲管注水的时间是28/1=28(小时)。4从“最不利”的情况入手。例4一把钥匙只能开一把锁,现在有4把钥匙和4把锁,但不知哪把钥匙开哪把锁,最多试多少次可以保证打开所有的锁?(贵阳市第二届小学数学竞赛试题)分析与解:要想“保证”在最少的次数内打开所有的锁,可以从“最不利”的情况入手。当开第一把锁时,如果最不凑巧,试了3次还没能打开,则第4把钥匙就一定能打开这把锁,这时能保证第一把锁配对钥匙,最多试3次。同样,能保 解较复杂的应用题应从哪里入手,http://www.guaimaomi.com对于一些比较复杂的应用题,学生在解答时往往不知该从哪里人手。下面,就解较复杂应用题引导学生该从哪里突破谈几点做法,以便学生在解题时做到有的放矢。少走弯路。 1 从全局入手。 例1 A、B两地相距1500米,甲、乙两人同时从两地相对而行,甲每分钟走72米,乙每分钟比甲多走6米,甲带着一条狗一起出发,狗每分钟跑300米,当狗遇见乙时,转身向甲方向跑,遇见甲时再转身往乙方向跑,如此往返。当甲、乙两人相遇时,这条狗共跑了多少千米? 分析与解:如果一段一段地求狗跑的距离,难以解答。可从全局考虑,狗不停地跑,甲、乙两人相遇时停止,狗跑的时间就是甲、乙两人相遇的时间,即1500·(72+6+72)=10(分钟)。从出发到相遇,狗每分钟跑300米,甲、乙两人相遇时,狗共跑了300×10=3000(米),即3千米。 2 从整体构造入手。 例2 甲、乙两列火车分别从A、B两城同时相对开出。经过5小时相遇。列车分别到达B、A城后,各休息2小时,再往回开。已知两列火车往返中速度不变,问从原地出发到第二次相遇,共经过多少小时? 分析与解:按照常规思路,设未知数列方程。将会碰到较大麻烦。现从整体上考虑,两列火车从开始到第二次相遇共走了A、B 间的三个单程,而合走一个单程要5小时,所以共需要5×3+2=17(小时)。 3 从份数入手。 例3 甲管注水速度是乙管的一半,同时开放甲、乙两个水管向池中注水,16小时可以注满。现在先开甲管向池中注水若干小时,剩下的由乙管注10小时将池注满。问:甲管注水的时间是多少小时? 分析与解:设甲管1小时的注水量为1份,则甲、乙两管的注水量为(1+2)×16=48(份)。因为乙管10小时注水2×10=20(份),所以甲管先注水48-20=28(份),即甲管注水的时间是28/1=28(小时)。 4 从“最不利”的情况入手。 例4 一把钥匙只能开一把锁,现在有4把钥匙和4把锁,但不知哪把钥匙开哪把锁,最多试多少次可以保证打开所有的锁?(贵阳市第二届小学数学竞赛试题) 分析与解:要想“保证”在最少的次数内打开所有的锁,可以从“最不利”的情况入手。当开第一把锁时,如果最不凑巧,试了3次还没能打开,则第4把钥匙就一定能打开这把锁,这时能保证第一把锁配对钥匙,最多试3次。同样,能保证第二把锁配对钥匙最多要试2次,第三把锁配对钥匙最多要试1次,第四把锁就不用试了,一定能打开。所以,要保证4把锁和4把钥匙一一配对,最多要试的次数为3+2+1+0=6(次)。 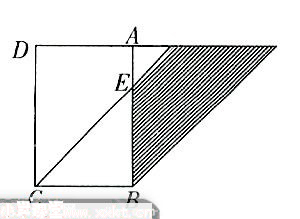
5 从因果关系入手。 例5用一个杯子向一个空瓶里倒水。如果倒进2杯水,连瓶共重360克;如果倒进5杯水,连瓶共重600克。想一想:一杯水和一个空瓶各重多少克? 分析与解:我们先把两次倒水的情况作一次比较。从连瓶重来看,第二次比第一次重了600-360=240(克),怎么会多240克呢?因为第二次比第一次多倒了5-2=3(杯)水。这样,就容易求出每杯水的重量为240/3=80(克),从而可得空瓶的重量为360-80×2=200(克)或600-80×5=200(克)。 6 从侧面入手。 例6右图中的四边形ABCD是长方形,AB=20厘米,AD=10厘米。BE=12厘米,阴影部分是一个梯形,求这个阴影部分的面积。 分析与解:通常求一个梯形的面积,需要知道上底、下底和高的长度,而此题中这三个条件都无法求出。怎么办呢?通过观察发现,右边的平行四边形与长方形的面积相等,因此阴影部分面积与直角梯形ADCE 
标签:解题研究,小学数学教学大全,小学数学教学网,小学数学教学 - 解题研究
上一篇:“换方问题”解法之我见
关键词:
|
最新《解题研究》
热门《解题研究》
|
Copyright 乖猫咪学习网 All Right Reserved.
